Gaussian Mixture Model

From K-means we know that:

• K-means forces clusters to be spherical
• In K-means clustering every point can only belong to one cluster

But sometimes it might be desirable to have elliptical clusters than spherical clusters. And what if there is a data point right in the center of two clusters?

Gaußian Mixture Model

With a random variable $X$, the mixed Gaussian model can be expressed by:

$p(x)=\sum_{k=1}^{K} \pi_{k} \mathcal{N}\left(X | \mu_{k}, \Sigma_{k}\right)$

where $\mathcal{N}\left(X | \mu_{k}, \Sigma_{k}\right)$ is the $k^{th}$ component of the mixture model.

Generalized Form

Then we can generate a generalized form:

$p(X | M, \Sigma, \pi)=\prod_{i=1}^{s} \sum_{k=1}^{K} \pi_{k} \mathcal{N}\left(x_{i} | \mu_{k}, \Sigma_{k}\right)$

$\text{for} \quad \mathcal{N}\left(x_{i} | \mu_{k}, \Sigma_{k}\right)=\frac{1}{\sqrt{(2 \pi)^{n} \operatorname{det}\left(\Sigma_{k}\right)}} e^{-\frac{1}{2}\left\langle\Sigma_{k}^{-1}\left(x_{i}-\mu_{k}\right), x_{i}-\mu_{k}\right\rangle}$

where

$X=\left( \begin{array}{llll}{x_{1}} & {x_{2}} & {\dots} & {x_{s}}\end{array}\right) \in \mathbb{R}^{n \times s} \quad \text { input data }$

$M=\left( \begin{array}{llll}{\mu_{1}} & {\mu_{2}} & {\dots} & {\mu_{K}}\end{array}\right) \in \mathbb{R}^{n \times K} \quad \text { prototype vectors }$

$\Sigma=\left(\Sigma_{1} \quad \Sigma_{2} \quad \ldots \quad \Sigma_{K}\right) \in \mathbb{R}^{n \times n \times K} \quad \text { covariance matrices }$

$\pi=\left( \begin{array}{llll}{\pi_{1}} & {\pi_{2}} & {\dots} & {\pi_{K}}\end{array}\right) \in \mathbb{R}^{K \times 1} \quad \text { mixing weights}$

$\text { and } \quad \pi_{k} \geq 0 \quad \text { for all } \quad k \in\{1, \ldots, K\} \quad \text { as well as } \sum_{k=1}^{K} \pi_{k}=1$

Now the goal for the algorithm is: given $X$ , determine the parameters $M$, $Σ$ and $π$ (for example by maximizing the likelihood)

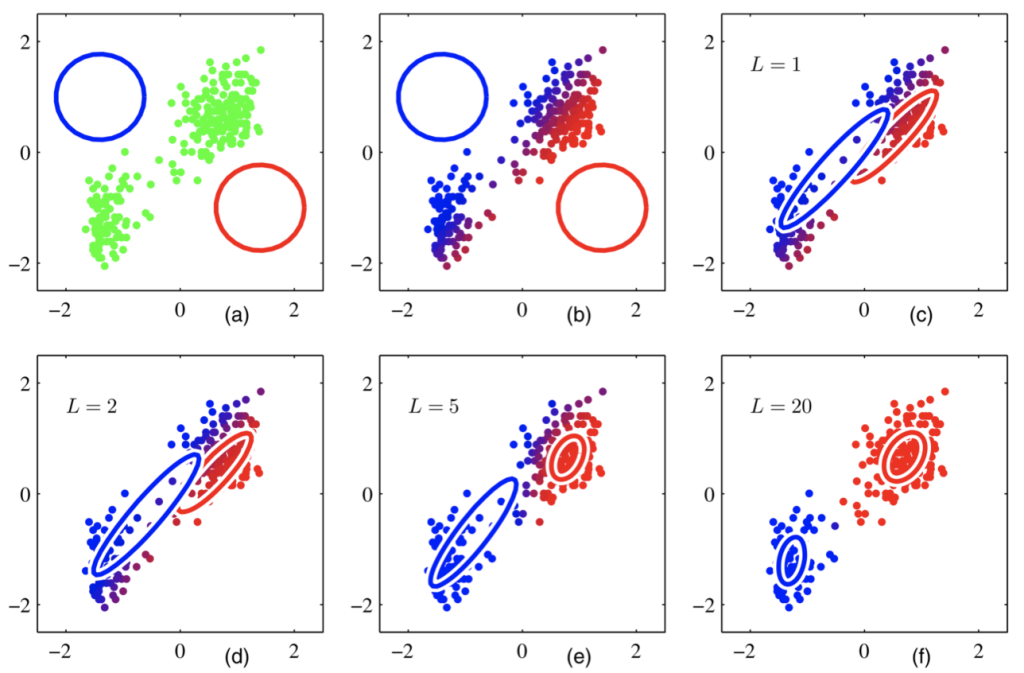
Model Iteration Illustration